Une (très) brève histoire de l’infini
- L’infini est un concept mathématique qui nous vient de Zénon d’Elée (~450 av. J.-C.) qui tenta de montrer son impossibilité « physique ». Il en résultera le « paradoxe de la flèche », résolu bien plus tard.
- De nombreux mathématiciens et physiciens vont alors tenter de comprendre l’infini et de l’expliquer par diverses théories et expériences.
- Georg Cantor ira plus loin que quiconque en se posant une question simple : Peut-on comparer deux ensembles infinis ? L’un peut-il être plus « grand » que l’autre ?
- Sa méthode consiste à mettre par paire un élément du premier ensemble avec un élément du deuxième. Si chaque élément trouve son partenaire et qu’aucun ne reste seul (on appelle ça une bijection), on peut alors dire que les deux ensembles sont égaux.
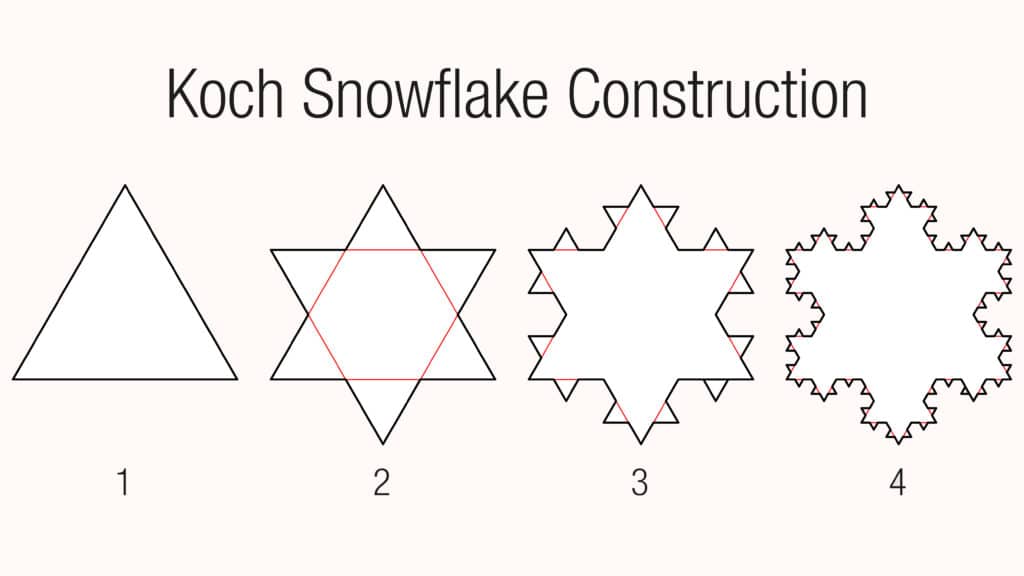
- Le flocon de Von Koch se construit en rajoutant un triangle sur chaque arête de la figure précédente et possède, de fait, un périmètre infini.
Considéré à une autre époque comme un concept sacré (seul Dieu est infini) ou métaphysique (l’esprit humain ne pourra jamais le concevoir entièrement), l’infini est depuis entré de plain-pied dans le domaine des sciences et des techniques. Aujourd’hui, on le mesure, on le compare, on l’étudie et l’utilise presque comme un nombre normal.
Mais qu’est-ce que l’infini ? Et comment a‑t-on appris à l’apprivoiser ?
Une vieille histoire
Il semble que le questionnement sur l’infini soit aussi vieux que l’humanité. Malheureusement, les écrits qui l’attestent sont d’autant plus rares qu’ils sont anciens. On sait que les philosophes du 1er millénaire avant Jésus-Christ s’émerveillaient déjà sur les propriétés étonnantes de l’infini.
Mais l’infini n’est-il qu’un concept ? Une idée bizarre avec laquelle jouent les mathématiciens ? Ou a‑t-il un lien avec le monde qui nous entoure ? Existe-t-il quelque chose de réellement infini ?
Pour Anaximandre, l’infini est le principe fondateur de la réalité. De lui naissent un nombre infini de mondes qui emplissent le volume de l’Univers. Pour Héraclite, par contre, c’est le temps qui est infini. Il a toujours été et sera toujours. C’est à travers lui que nous percevons notre propre existence.
Bien sûr, aucune de ces affirmations n’est étayée par une « expérience » ou une « mesure » telles que nous les concevons aujourd’hui dans la démarche scientifique. Il s’agit plus d’une position philosophique qui différencie une école de pensée d’une autre.
Des mathématiques à la physique
L’infini est d’abord et avant tout un concept mathématique. Et ce sont les mathématiciens qui s’en emparent pour l’observer à la loupe. Zénon d’Elée (~450 av. JC) tente de montrer l’impossibilité « physique » de l’infini, non plus en le mesurant, mais au contraire en s’en servant pour diviser les choses en éléments toujours plus petits.
Il en résulte son célèbre « paradoxe » de la flèche qui, selon lui, ne devrait jamais pouvoir atteindre sa cible. En effet, on peut toujours diviser son parcours restant par deux et il restera toujours une portion de chemin à parcourir (1/2, 1/4, 1/8, 1/16, 1/32), à l’infini.
Dans la mesure où il faut un nombre infini d’étapes pour franchir la distance entre l’arc et la cible, Zénon conclut à l’impossibilité à la flèche d’atteindre sa destination en un temps fini.
Ce paradoxe fut résolu bien plus tard par une des branches des mathématiques qui étudie les sommes infinies de nombres : les séries.
Ajouter 1/2+ 1/4+ 1/8+ 1/16+… revient à faire la somme 1/2+ 1/2²+ 1/23+ 1/24+…
Cette série s’appelle une série géométrique. Elle s’écrit sous la forme :

Sa résolution est très simple. Lorsque n tend vers l’infini, la valeur de cette somme tend naturellement vers 1.
Sa résolution graphique est encore plus simple. Dans la figure ci-dessous, on voit intuitivement que, pour remplir un carré de côté 1, il faut faire la somme d’éléments dont l’aire correspond exactement à la série ci-dessus.
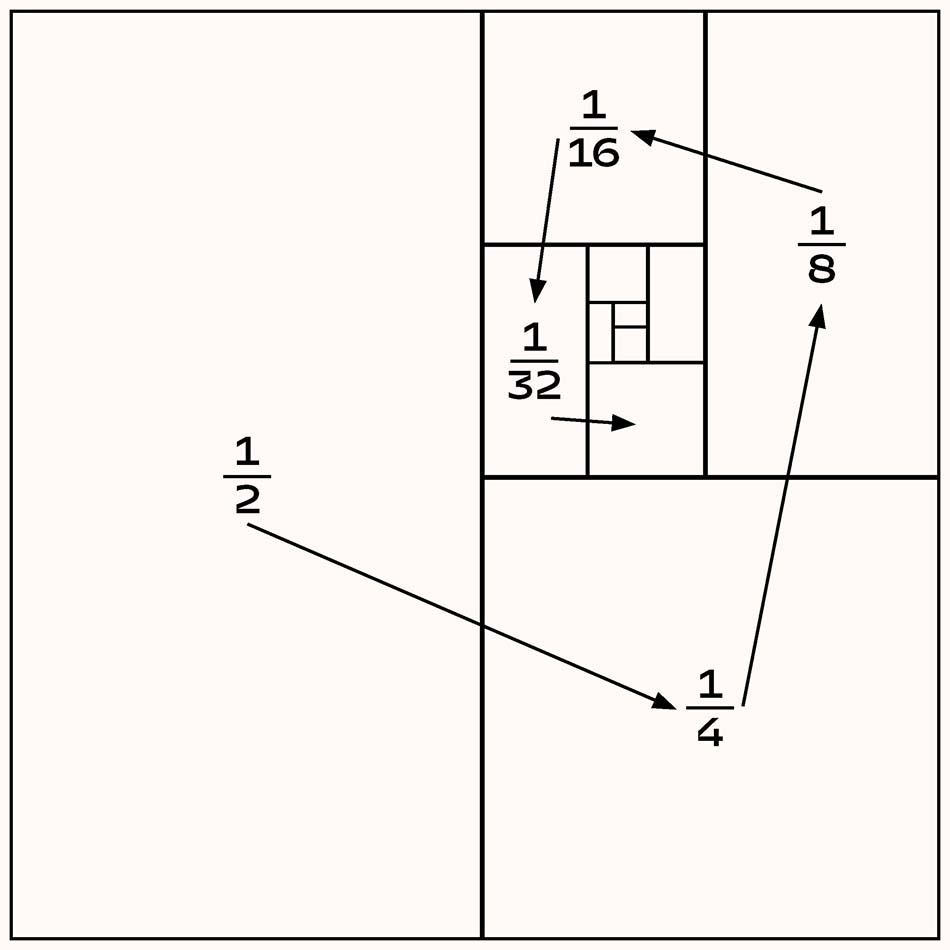
Ce qu’il manquait à Zénon, c’est ce résultat contre-intuitif que la somme d’une infinité de nombres ne donne pas toujours un résultat infini.
Autrement dit, ce n’est pas parce que la trajectoire de la flèche peut être décomposée en un nombre infini que le temps qu’elle mettra pour les parcourir sera infini. Paradoxe résolu. Les flèches peuvent désormais rejoindre leur cible en toute quiétude.
Plus tard, le célèbre Isaac Newton perfectionnera l’art de mesurer des valeurs arbitrairement petites en développant le calcul infinitésimal. Celui-ci débouche sur les célèbres dérivées (et intégrales) dont les mathématiques, mais aussi la physique moderne, ne sauraient se passer aujourd’hui pour décrire et comprendre le monde.
Comparer les infinis
Nul besoin de comprendre ni de visualiser l’infini pour s’en servir. L’infini n’est finalement qu’un outil parmi bien d’autres que les mathématiques mettent à notre disposition pour mesurer, calculer et appréhender notre environnement.
Mais un mathématicien allemand de la fin du XIXème siècle est allé bien plus loin que quiconque à l’époque pour manipuler l’infini, ou plus précisément les ensembles infinis.
Georg Cantor se pose alors une question simple : Peut-on comparer deux ensembles infinis ? L’un peut-il être plus « grand » que l’autre ?
Sa réponse tient dans la manière utilisée pour comparer deux ensembles : au lieu de compter le nombre d’éléments de ces derniers et de les comparer (ce que l’on ne peut pas faire avec un ensemble infini), la méthode consiste à essayer d’apparier un élément du premier ensemble avec un élément du deuxième. Si chaque élément trouve son partenaire et qu’aucun ne reste seul (on appelle ça une bijection), on peut alors dire que les deux ensembles sont égaux. Et cette méthode s’applique aussi bien à des ensembles finis et infinis.
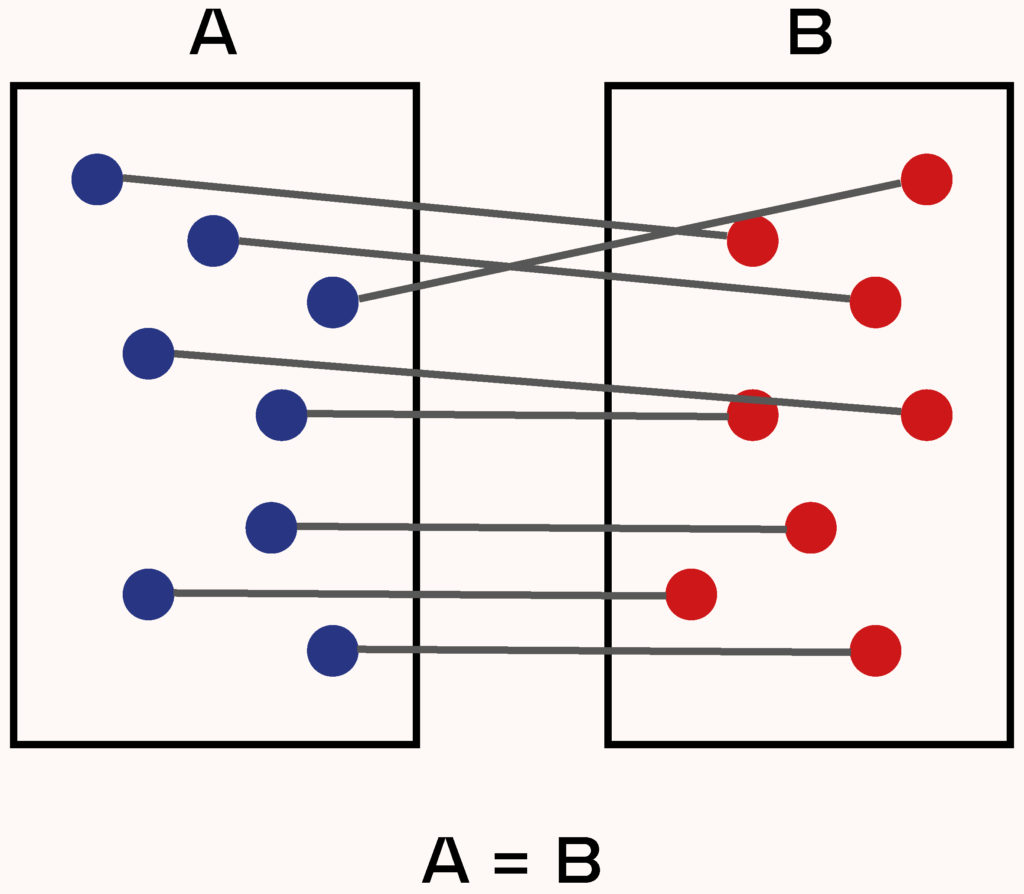
C’est ainsi que l’on peut prouver que la taille de l’ensemble (infini) des entiers positifs est strictement égale à celle de l’ensemble des entiers (positifs et négatifs).
Plus fort, on a pu aussi montrer que, bien qu’il y ait une infinité de fractions entre deux entiers, la taille de l’ensemble des entiers est rigoureusement égale à celle de l’ensemble des nombres qui s’écrivent sous forme de fraction.
Cependant, il a aussi été prouvé que l’ensemble des nombres réels (tous les nombres s’écrivant avec une virgule et un nombre fini ou infini de décimales) était strictement supérieur à celui des entiers.
Aussi contre-intuitif que cela puisse paraître, deux infinis différents peuvent avoir la même taille, mais, à l’inverse, tous les infinis ne se valent pas.
Des géométries impossibles
Peut-on dessiner des figures dont certains paramètres sont infinis ?
Outre le cercle (dont on peut considérer qu’il s’agit d’un polygone avec un nombre infini de côtés), d’autres figures étranges ont commencé à émerger pendant la 2ème moitié du XXème siècle : les fractals.
Une manière de les créer est de les construire par itération, étape par étape. Au bout d’un nombre infini d’étapes, la figure est terminée, et on peut en étudier les propriétés.
Le flocon de Von Koch, par exemple, est une figure extraordinaire : bien que sa surface soit finie, son périmètre, lui est infini.
Ce genre de géométrie a été appliqué avec succès dans le domaine des télécommunications. Depuis la fin des années 80, on développe ainsi des antennes fractales, dont la longueur, à défaut d’être infinie, est très grande, mais dont le volume reste faible, ce qui permet d’obtenir des systèmes compacts et efficaces.