Trous noirs : sont-ils stables ?

Ein­stein ne croyait pas aux trous noirs, mais les obser­va­tions (indi­rectes) des années 2010 lui donnent tort : les trous noirs sont bel et bien réels. Véri­tables super­stars de la science moderne, ils fas­cinent bien au-delà des com­mu­nau­tés aca­dé­miques qui les étu­dient. Tour d’horizon d’un siècle de trous noirs, des pre­miers cal­culs de Schwarz­schild aux récents tra­vaux de Szef­tel et Klainerman.

His­to­ri­que­ment, les trous noirs ont d’abord été des objets mathé­ma­tiques, sous- pro­duits inat­ten­dus de la théo­rie de la rela­ti­vi­té géné­rale. Cette der­nière, publiée en 1915 par Albert Ein­stein, révo­lu­tion­na notre concep­tion de la gra­vi­ta­tion et de l’espace qui nous entoure. Dans cette théo­rie, l’espace et le temps forment un conti­nuum qui pos­sède une géo­mé­trie propre. En par­ti­cu­lier, l’espace-temps peut se cour­ber sous l’action de la matière, a l’image d’un drap sup­por­tant un objet lourd. Pour décrire cette cour­bure, Ein­stein énonce une équa­tion qui porte aujourd’hui son nom :

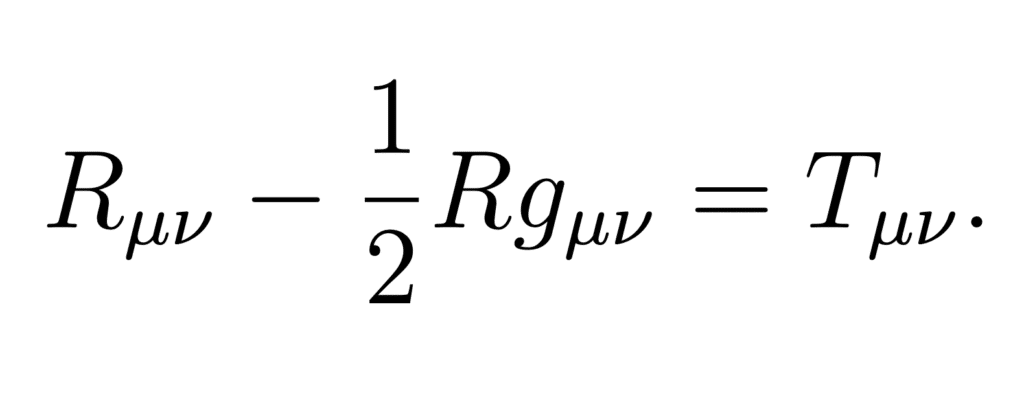
Quelques mois seule­ment après ces publi­ca­tions, le phy­si­cien alle­mand Karl Schwarz­schild, alors mobi­li­sé sur le front russe de la Grande guerre, découvre une solu­tion par­ti­cu­lière à ces équa­tions. Appe­lée la métrique de Schwarz­schild, elle décrit l’espace-temps au voi­si­nage d’un corps à symé­trie sphé­rique, comme une étoile ou une pla­nète. Si la den­si­té de ce corps dépasse un cer­tain seuil, il s’agit d’un trou noir. La den­si­té d’un tel objet est tout bon­ne­ment déli­rante : pour trans­for­mer la Terre en trou noir, il fau­drait la faire ren­trer dans une pis­tache ! Les trous noirs sont tel­le­ment denses que rien ne peut leur échap­per : une fois pas­sé leur fron­tière, l’horizon des évè­ne­ments, tout objet res­te­ra à jamais empri­son­né. Cela s’applique aus­si à la lumière ! Ain­si, les trous noirs n’émettent aucune lumière, d’où leur nom.

Pro­blème : toutes nos obser­va­tions astro­no­miques se fondent sur l’étude de la lumière venue du cos­mos, récu­pé­rée par des téles­copes ou par nos yeux. Pour obser­ver des trous noirs, il faut donc ruser !

Une solu­tion radi­cale consiste à ne plus s’intéresser aux ondes lumi­neuses et à détec­ter les ondes gra­vi­ta­tion­nelles. Autre pré­dic­tion spec­ta­cu­laire de la rela­ti­vi­té géné­rale, ces vagues de l’espace-temps sont la trace de phé­no­mènes cata­clys­miques tels que la fusion de deux trous noirs. Elles se pro­pagent à la vitesse de la lumière et nous pou­vons détec­ter leur pas­sage grâce aux inter­fé­ro­mètres géants de la col­la­bo­ra­tion LIGO-VIRGO. Ces détec­teurs d’envergure kilo­mé­trique ont per­mis en 2015 la pre­mière obser­va­tion indi­recte des trous noirs.

La pre­mière pho­to­gra­phie d’un trou noir, quant à elle, date de 2019. Dans ce cas, ce n’est pas le trou noir que l’on observe mais le disque com­po­sé de matière incan­des­cente prête à se faire dévo­rer orbi­tant autour de l’astre géant.

Bien avant qu’une obser­va­tion ne serait-ce qu’indirecte ne puisse être envi­sa­gée, les mathé­ma­tiques consti­tuaient le meilleur outil pour s’attaquer aux mys­tères entou­rant les trous noirs. En haut de la liste figu­rait la ques­tion de la for­ma­tion des trous noirs. Quel méca­nisme peut accou­cher de tels monstres ?

Dans les années 1960, le physicien/mathématicien Roger Pen­rose tra­vaille sur cette ques­tion et démontre son théo­rème de for­ma­tion des sin­gu­la­ri­tés¹. Ce der­nier sti­pule que la sin­gu­la­ri­té au centre des trous noirs, catas­tro­phique du point de vue de la cau­sa­li­té, se forme néces­sai­re­ment si l’espace-temps satis­fait loca­le­ment des condi­tions de cour­bure très forte. De telles condi­tions peuvent être réunies lors de l’effondrement gra­vi­ta­tion­nel d’une étoile en fin de vie, pro­vo­qué par l’épuisement de son car­bu­rant. Ces tra­vaux valent à Pen­rose le prix Nobel de phy­sique 2019, et per­mirent de com­prendre que la mort d’une étoile peut déclen­cher la nais­sance d’un trou noir.

Les pro­grès tech­niques de l’astronomie moderne nous per­mettent d’observer des astres tou­jours plus loin­tains, et ain­si son­der leur pas­sé. On peut donc espé­rer obser­ver la nais­sance, ou tout du moins la jeu­nesse, des trous noirs. Mais une autre ques­tion de taille échappe à nos téles­copes : le futur des trous noirs. En par­ti­cu­lier, sont-ils stables ?

En phy­sique, on pré­fère les objets stables aux objets instables. Ima­gi­nez une boule pla­cée au som­met d’une col­line : si on la pousse légè­re­ment, elle dévale la pente ! Le som­met de la col­line est donc une posi­tion instable, qui ne résiste pas à de petites per­tur­ba­tions. A l’inverse, on peut se convaincre que le fond d’un trou est une posi­tion stable. Le téles­cope spa­tial James Webb illustre à mer­veille ces concepts : il a pour des­ti­na­tion le point de Lagrange L2, posi­tion stable sous per­tur­ba­tion angu­laire, mais instable sous per­tur­ba­tion radiale…

La ques­tion de la sta­bi­li­té des trous noirs se for­mule alors ain­si : qu’arrive- t‑il à une solu­tion de Schwarz­schild repré­sen­tant un trou noir si elle est légè­re­ment per­tur­bée ? Revient-elle à l’équilibre comme la boule au fond du trou ? Oui, selon deux longs articles récents²³ par les mathé­ma­ti­ciens Jéré­mie Szef­tel et Ser­giu Klai­ner­man. Abou­tis­se­ment de dix années de recherche, leur démons­tra­tion repose sur une com­pré­hen­sion fine de la géo­mé­trie des trous noirs, ain­si que sur le déve­lop­pe­ment de nom­breuses tech­niques d’analyse des équa­tions aux déri­vées partielles.

La réso­lu­tion de la conjec­ture de sta­bi­li­té des trous noirs par Szef­tel et Klai­ner­man est un exploit mathé­ma­tique majeur, mais leurs tra­vaux ne marquent pas la fin de l’histoire, bien au contraire. Leur objec­tif ultime porte le doux nom de conjec­ture de l’état final. En des termes simples, elle sti­pule que dans un futur extrê­me­ment loin­tain, l’univers ne sera consti­tué que de trous noirs s’éloignant les uns des autres. Dans ce scé­na­rio, si deux trous noirs sont trop proches, ils fusionnent en libé­rant des ondes gravitationnelles.

Démon­trer mathé­ma­ti­que­ment cette conjec­ture néces­site de résoudre de nom­breuses ques­tions inter­mé­diaires, dont la conjec­ture de sta­bi­li­té des trous noirs. En effet, si tout le conte­nu de notre uni­vers converge à terme vers des trous noirs, il faut que les trous noirs eux-mêmes « convergent vers eux-mêmes », c’est-à-dire qu’ils soient stables ! Une autre « sous-conjec­ture » est celle de la cen­sure cos­mique, intro­duite par Pen­rose en 1969, qui pré­dit que les sin­gu­la­ri­tés telles que celles que l’on trouve au centre des trous noirs ne peuvent être « nues », c’est-à-dire exis­ter sans un hori­zon des évè­ne­ments autour d’elles qui pro­tège l’univers de leur carac­tère paradoxal.

La conjec­ture de l’état final et la plu­part de ses « sous-conjec­tures » sont  encore hors de por­tée aujourd’hui. Elles occu­pe­ront sûre­ment les mathé­ma­ti­ciennes et mathé­ma­ti­ciens de la rela­ti­vi­té géné­rale pen­dant des dizaines, voire des cen­taines d’années. Mal­gré ses ten­ta­tives pour décrire la fin de l’univers, la recherche phy­si­co- mathé­ma­tique est réel­le­ment sans fin.

Pour en savoir plus 

Voyage au Coeur de l’Espace-Temps, Sté­phane d’Ascoli et Arthur Toua­ti (2021), First Edi­tions