Il paraît que le télescope spatial James Webb vient tout juste d’arriver à « bon port », au fameux « point de Lagrange L2 » dans le vide interplanétaire de notre système solaire, à quelques 1,5 million de kilomètres de la Terre. Pourquoi les agences spatiales ont-elles décidé de le positionner à cet endroit ? Qu’ont ces « points » de Lagrange de si particulier pour y envoyer des satellites depuis 50 ans ?
Le problème des trois corps
Depuis les lois de la mécanique et de la gravitation élaborées par Isaac Newton à la fin du XVIIe siècle, le « problème des trois corps », qui consiste à déterminer le mouvement de trois objets célestes sous leurs seules attractions gravitationnelles mutuelles, est un des plus fructueux problèmes de physique. Les tentatives pour le résoudre ont permis le développement d’innombrables avancées théoriques, elles-mêmes responsables d’applications pratiques révolutionnaires. Même si, aujourd’hui, et notamment grâce aux travaux d’Henri Poincaré à la fin du XIXe siècle, on comprend mieux pourquoi il est difficile, on peut encore considérer qu’il n’est, à ce jour, pas complètement résolu.
Les points de Lagrange apparaissent naturellement comme des solutions particulières du problème à trois corps dit « restreint », dans lequel l’un des corps est tout petit comparé aux deux autres. C’est le cas du mouvement d’un satellite autour du Soleil et d’une planète. Nous nous plaçons dorénavant dans ce cadre.
L’équilibre des forces
Considérons d’abord le mouvement de la Terre autour du Soleil, qui est un cercle quasi-parfait. Elle en fait le tour en un an, c’est ce que l’on appelle sa période de révolution. Imaginons maintenant que l’on place un satellite en orbite circulaire autour du Soleil, avec une période de révolution d’exactement un an, et de sorte qu’il soit toujours placé sur l’axe Terre-Soleil. En ajustant sa distance au Soleil, la force d’attraction de ce dernier va exactement compenser celle de la Terre et le satellite sera à l’équilibre.
Mais le lecteur attentif aura remarqué que si le satellite orbite le Soleil, alors il subit aussi une force centrifuge (celle qui nous tire vers l’extérieur dans un manège ou un rond-point). Cette force s’ajoute aux attractions gravitationnelles, mais ne change pas la donne : on pourra toujours ajuster la position du satellite sur l’axe Soleil-Terre pour que les trois forces se compensent, comme représenté sur la figure ci-dessous.
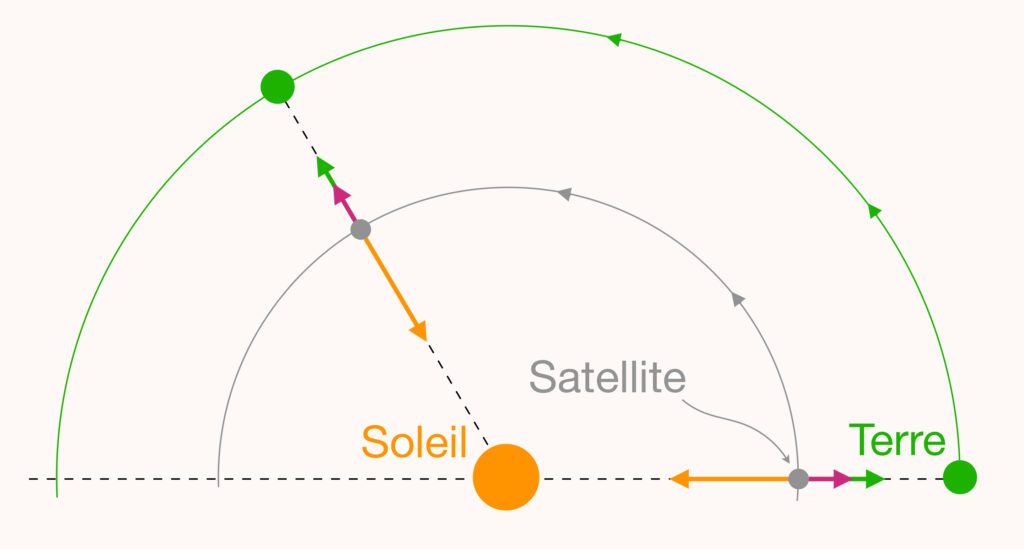
Le référentiel co-tournant
Cette orbite que nous venons de construire est précisément le premier de ce que les astronomes appellent un « point de Lagrange ». Mais alors pourquoi « point » et pas « orbite » de Lagrange ? La raison se trouve dans une autre manière de regarder notre problème. En effet, puisque le satellite et la Terre font une révolution complète autour du Soleil en un an, on peut imaginer tourner avec eux, et prendre en compte cette révolution dans la représentation graphique du problème. La trajectoire du satellite est alors réduite à un point, placé entre le Soleil et la Terre, qui, elle aussi, est immobile dans ce référentiel dit « co-tournant ». Ce point, qui représente en fait une orbite, est le point de Lagrange L1.
Les trois premiers
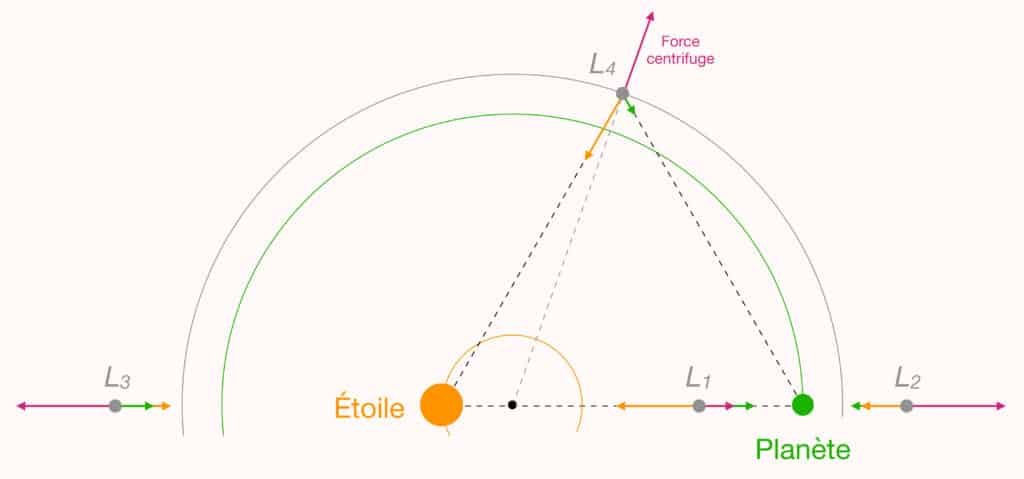
Le référentiel co-tournant est bien pratique et permet de découvrir quatre autres points de Lagrange, en cherchant d’autres endroit où les forces d’attraction de la Terre et du Soleil compensent la force centrifuge. Deux autres de ces points, appelés L2 et L3, se trouvent aussi sur l’axe Soleil-Terre, comme indiqué sur la figure ci-dessous.

L2 se situe de l’autre côté de la Terre par rapport à L1, et L3 est de l’autre côté du Soleil. On voit bien sur la figure que les trois forces subies par un satellite en ces points se compensent : c’est pourquoi on les appelle aussi des « points d’équilibre ». Avec L1, les points L2 et L3 correspondent à trois solutions exactes du problème à trois corps déterminées par Leonard Euler et publiées en 1765. En particulier, étant situé à l’opposé du Soleil par rapport à nous, le point L3 a été l’objet de nombreux fantasmes depuis l’antiquité, comme l’hypothétique anti-Terre qui serait placée en L3 et qui nous serait invisible, car cachée par le Soleil.
Satellites artificiels
Côté « pratique », c’est surtout les points de Lagrange L1 et L2 qui ont intéressé les agences spatiales. En effet, on y envoie régulièrement des satellites pour des missions scientifiques bien précises. La première fois, c’était en 1978 avec le programme ISEE (pour International Sun-Earth Explorer) dont les modules furent mis en orbite autour du point de Lagrange L1 du système Soleil-Terre (situé à 1,5 million de km, soit moins de 1% de la distance Terre-Soleil). Le point L1 du système Terre-Lune (à 326 000 km de la Terre, 15% de la distance Terre-Lune) accueille lui aussi depuis 2018 le satellite relais chinois Queqiao pour communiquer avec la sonde lunaire Chang’e 4 posée sur la face cachée de la Lune.
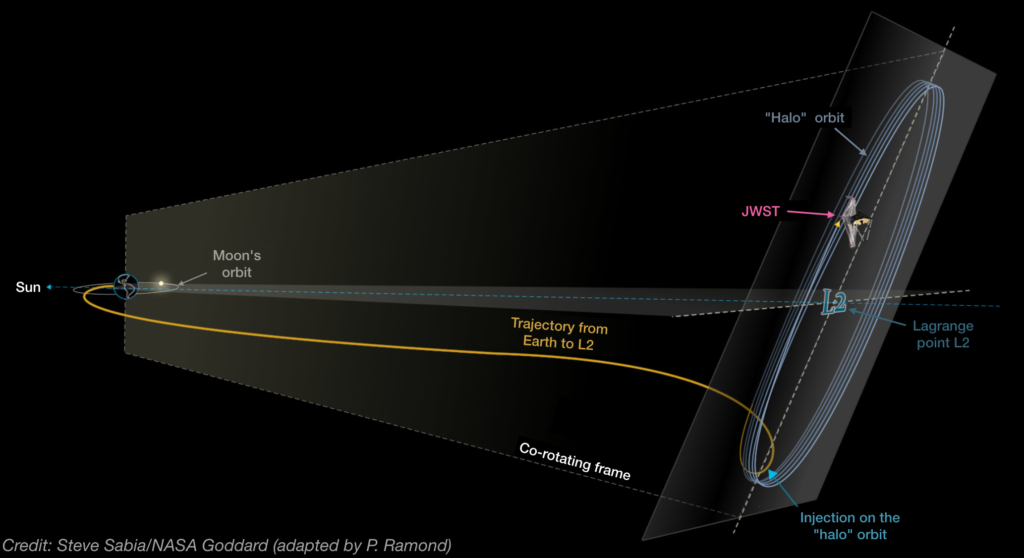
Mais c’est le point L2 du système Soleil-Terre qui est l’hôte des missions spatiales les plus extraordinaires (situé lui aussi à environ 1,5 million de km de la Terre). Parmi les plus récentes, on peut évoquer le satellite Planck1 lancé en 2009 pour mesurer avec une extrême précision la plus ancienne lumière de l’Univers (le fond diffus cosmologique). Le satellite LISA Pathfinder, lancé en 2015, avait lui pour but de démontrer la maturité de la technologie nécessaire au futur interféromètre gravitationnel spatial LISA. Plus récemment, la mission Gaïa2 qui catalogue position, vitesse et lumière de plus d’un milliard d’objets célestes (étoiles, mais aussi astéroïdes, galaxies, etc) à trouvé sa place en L2 lui-aussi. Le dernier satellite à rejoindre le point L2 est le télescope spatial James Webb3, lancé le 25 décembre 2021. Successeur du célèbre télescope Hubble, il a pour mission d’explorer les confins de l’Univers pour y observer les toutes premières galaxies, ainsi que l’étude des exoplanètes.
Mais alors, tous ces satellites au point L2 ne risquent-ils pas de se heurter ? Après-tout, il y a peu de place dans un « point » de Lagrange ! Heureusement, ces satellites sont envoyés non pas exactement à l’emplacement des points de Lagrange, mais en orbite autour d’eux, dans une zone couvrant une région extrêmement vaste à l’échelle d’un satellite : plusieurs centaines de milliers de kilomètres de diamètre. Les satellites sont ainsi en orbite autour du point de Lagrange, mais les quelques ajustements nécessaires pour les y maintenir sont dérisoire au regard de ce qu’il faudrait pour les maintenir sur une telle orbite ailleurs dans le système solaire. C’est là le principal intérêt des points de Lagrange : laisser la gravitation et la mécanique s’occuper « naturellement » du mouvement du satellite, pour que les astronomes n’aient qu’à se consacrer à la belle science qu’ils permettent de faire !
Les deux derniers
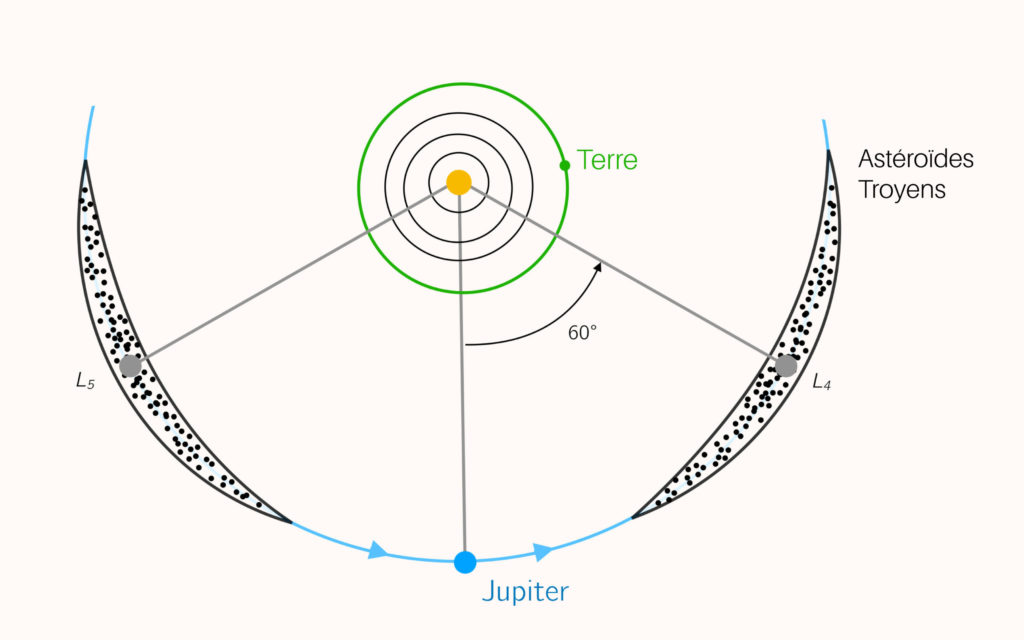
C’est Joseph-Louis Lagrange qui montra en 1772 que deux autres points, L4 et L5, existent. Ils ne sont pas sur l’axe Soleil-Terre, mais situés à égale distance d’eux, de telle sorte à former un triangle équilatéral. En ces points, les deux forces gravitationnelles et la force centrifuge, bien que non-alignées, se compensent parfaitement, comme indiqué sur la figure ci-dessous. En pratique, le satellite se situe donc quasiment sur l’orbite de la Terre, avec 60° d’avance (L4) ou de recul (L5) par rapport à elle.
Objets naturels
Les points de Lagrange étant associés à des positions d’équilibre, il ne serait pas étonnant d’y trouver, dans le système Solaire, des objets naturels (comme des petits astéroïdes). Dans le cas du système Soleil-Jupiter, on observe autour des points de Lagrange L4 et L5 environ 10 000 astéroïdes à ce jour. Appelés astéroïdes Troyens, certains d’entre eux ont même des satellites naturels à leur tour, comme le plus gros appelé « (624) Hector » et sa lune astéroïdale « Scamandrios ».
Ces milliers d’objets sont la preuve que les régions de stabilité de Lagrange sont réelles et pas juste des considérations théoriques. La plupart des planètes du système Solaire ont des astéroïdes « Troyens », i.e., situé proche des emplacements L4 et L5 du système Soleil-planète, même s’il faut noter qu’aucun Troyen n’a été observé pour le système Terre-Saturne. On soupçonne que les perturbations dues à Jupiter empêche les astéroïdes d’y rester trop longtemps4. Ironiquement, deux satellites naturels de Saturne, Téthys et Dionné, possèdent des Troyens eux-mêmes !